Exploratory Data Analysis
The data set provided by the Swiss Link Market Research Institute. This is from a survey in which people got a questionnaire about their experiences with a restaurant. In particular, it is of interest to understand: 1. Which among the variables have the most influence on the overall satisfaction (g27a) 2. Whether some of them measure the same thing or are related to the same factor The data set has 1033 respondents and answers to 18 questions. The first question g27a is the overall quality assessment while the other variables refer to specific characteristics. Responses are coded on a scale between 1 (worst possible) and 10 (best possible). The answers that report an 11 (“doesn’t apply”) and a 12 (“no answer given”) are considered missing values.
| Overall (N=1033) | |
|---|---|
| General Satisfaction | |
| Mean (SD) | 7.97 (1.64) |
| Median (Range) | 8.00 (1.00, 10.00) |
| Good parking situation | |
| Mean (SD) | 8.32 (2.71) |
| Median (Range) | 10.00 (1.00, 12.00) |
| Good to access by public transport | |
| Mean (SD) | 8.49 (2.98) |
| Median (Range) | 10.00 (1.00, 12.00) |
| Kindly placed at good table | |
| Mean (SD) | 8.68 (1.83) |
| Median (Range) | 9.00 (1.00, 12.00) |
| Choice on the menu | |
| Mean (SD) | 8.10 (1.82) |
| Median (Range) | 8.00 (1.00, 12.00) |
| Taste of food | |
| Mean (SD) | 8.50 (1.61) |
| Median (Range) | 9.00 (1.00, 12.00) |
| Meals large enough | |
| Mean (SD) | 9.00 (1.41) |
| Median (Range) | 10.00 (2.00, 12.00) |
| Quality of ingredients | |
| Mean (SD) | 8.70 (1.62) |
| Median (Range) | 9.00 (1.00, 12.00) |
| Quality of general service | |
| Mean (SD) | 8.16 (1.86) |
| Median (Range) | 9.00 (1.00, 12.00) |
| Waiting time before payment | |
| Mean (SD) | 8.30 (1.92) |
| Median (Range) | 9.00 (1.00, 12.00) |
| Neat appearance of waiters | |
| Mean (SD) | 8.30 (1.81) |
| Median (Range) | 9.00 (1.00, 12.00) |
| Friendliness | |
| Mean (SD) | 8.66 (1.72) |
| Median (Range) | 9.00 (1.00, 12.00) |
| Competent information about food and drinks | |
| Mean (SD) | 8.63 (2.28) |
| Median (Range) | 9.00 (1.00, 12.00) |
| Atmosphere in the restaurant | |
| Mean (SD) | 7.86 (1.95) |
| Median (Range) | 8.00 (1.00, 12.00) |
| Air quality/freshness | |
| Mean (SD) | 7.97 (2.08) |
| Median (Range) | 8.00 (1.00, 12.00) |
| Restaurant clean | |
| Mean (SD) | 8.58 (1.65) |
| Median (Range) | 9.00 (1.00, 12.00) |
| Comfortable chairs | |
| Mean (SD) | 7.91 (1.98) |
| Median (Range) | 8.00 (1.00, 12.00) |
| Correctness of bill | |
| Mean (SD) | 9.32 (1.44) |
| Median (Range) | 10.00 (1.00, 12.00) |
Dealing with Missing Values
At this phase we have to deal with missing values as the codings corresponding to 11 and 12 corresponds to missing data, so first all I’ve highlighted the NA in the dataset. Moreover, by dropping the observations completely, we do not only lose statistical power, but we may even get biased results as the dropped observations could provide crucial information about the problem of interest, so it would be a pity to simply ignore them.
gg_miss_var(restaurant, show_pct = T) +
labs(
title = "Number of Missing Values in the Survey",
subtitle = "Answers 11 & 12",
caption = "Data: Swiss Link Market Research",
x = "Questions",
y = "% Missing Values") +
scale_y_continuous(breaks = seq(from = 0, to = 300, by = 5)) +
theme(
plot.title = element_text(
hjust = 0.5, # center
size = 12,
color = "steelblue",
face = "bold"),
plot.subtitle = element_text(
hjust = 0.5, # center
size = 10,
color = "gray",
face = "italic"))## Warning: It is deprecated to specify `guide = FALSE` to remove a guide. Please
## use `guide = "none"` instead.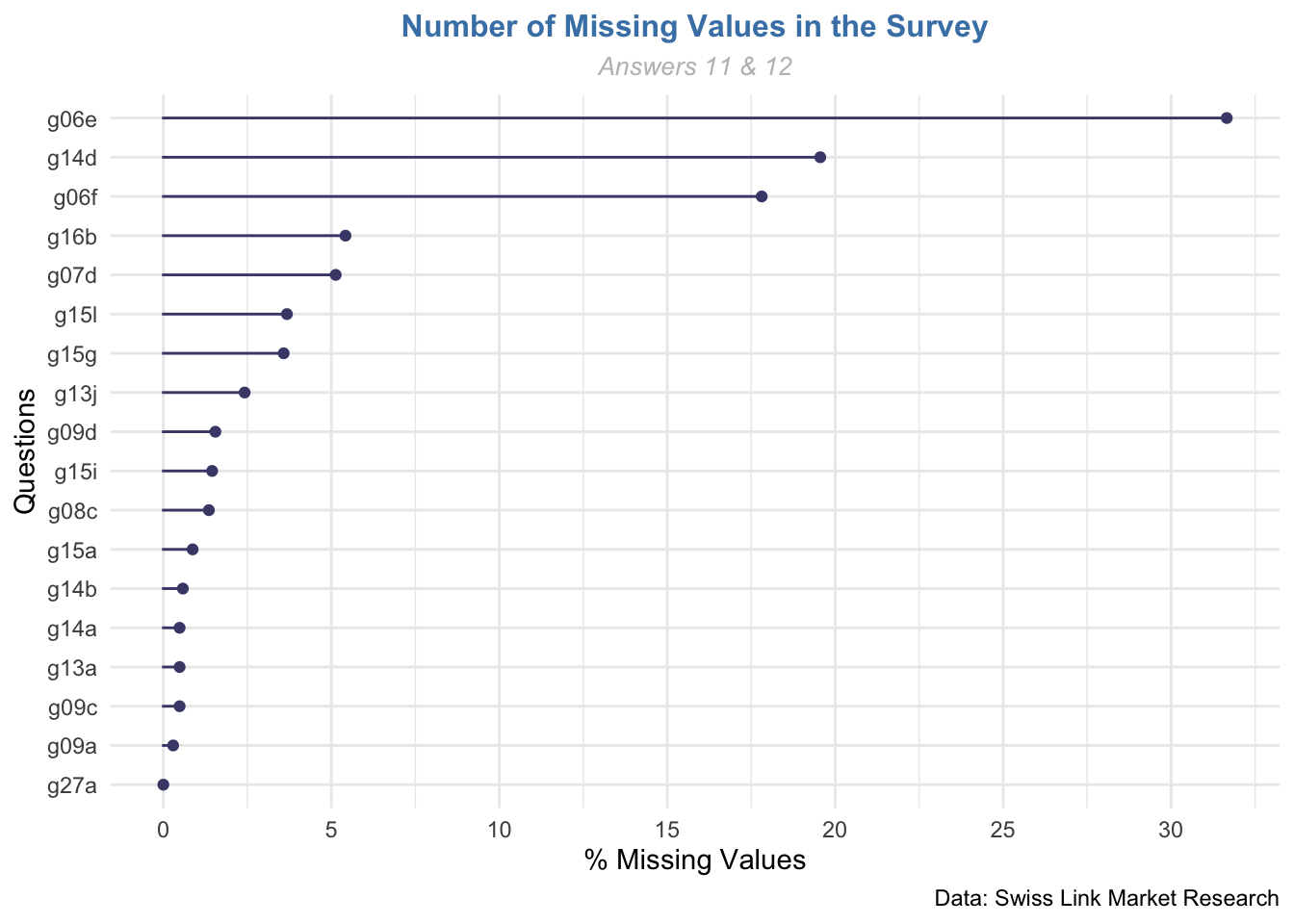
Thus the variable which present more number of missing values are:
- g06e - Good to access by public transport (31,7%)
- g14d - Competent information about food and drinks (19,6%)
- g06f - Good parking situation (17,8%)
The fact that two questions belonging to the same group of variables have the higher percentage of missing values may not be casual. Now is the presence of missing values related with missings between variables?
# Which combinations of variables occur to be missing together?
gg_miss_upset(restaurant) 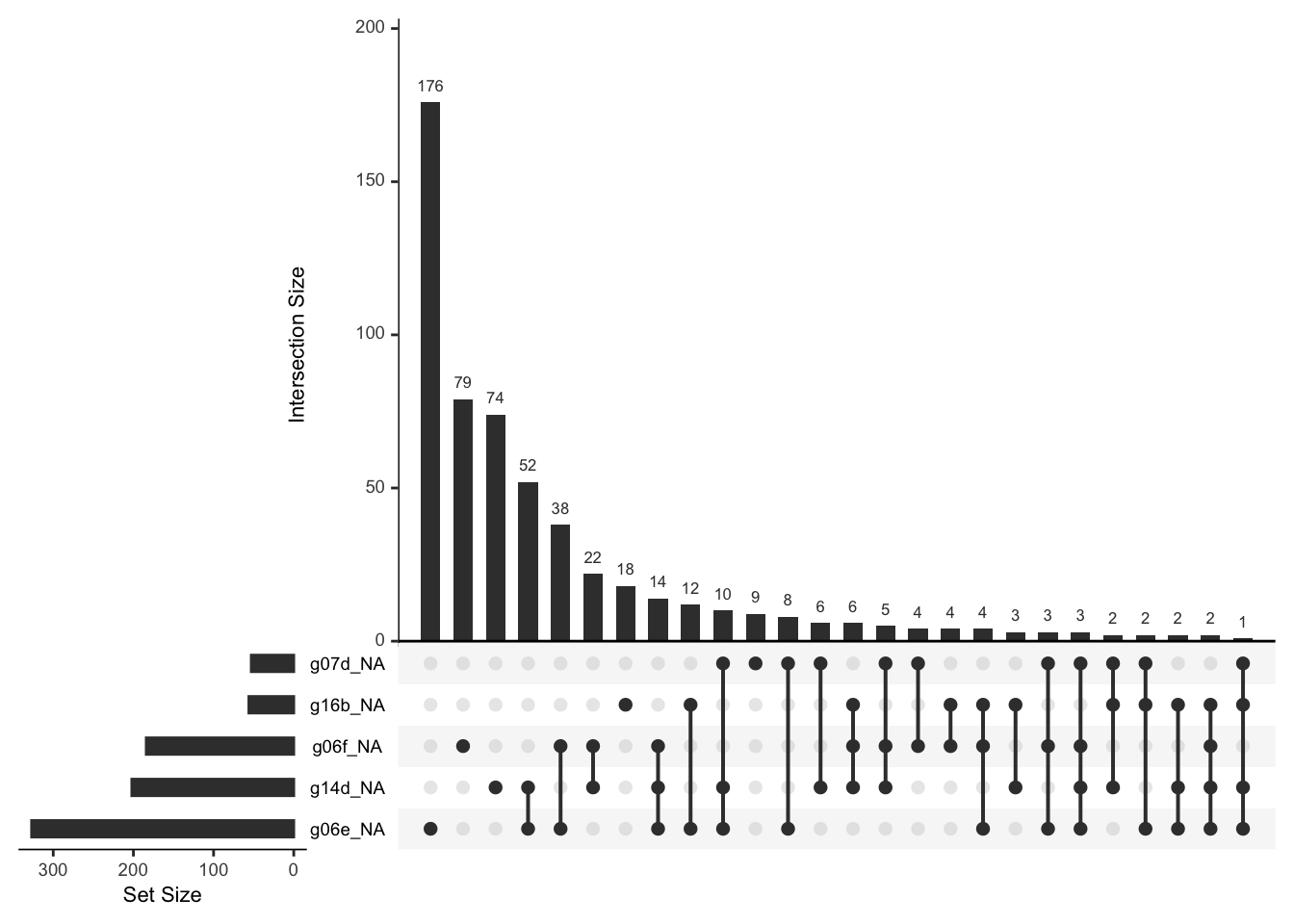
There is a substantial number of cases in which some missings happen to occur across these two variables (=38), so this is a sign that data is not missing at random, I suppose we’re dealing with MAR.
Imputation for NAs and Diagnostic Visualization Tools
Before fitting a model, even if by default the function will exclude the NAs, but this would leave the analysis with few data. I’m going to perform a Regression Imputation . A regression model is estimated to predict observed values of a variable based on other variables, and that model is then used to impute values in cases where the value of that variable is missing (through fitted values). It’s effective to use with non-missing information (MAR)
pred <- rest.imp$predictorMatrix
pred[,"g27a"] <- 0
stripplot(rest.imp, pch = 20, cex = 2, layout = c(3,6))
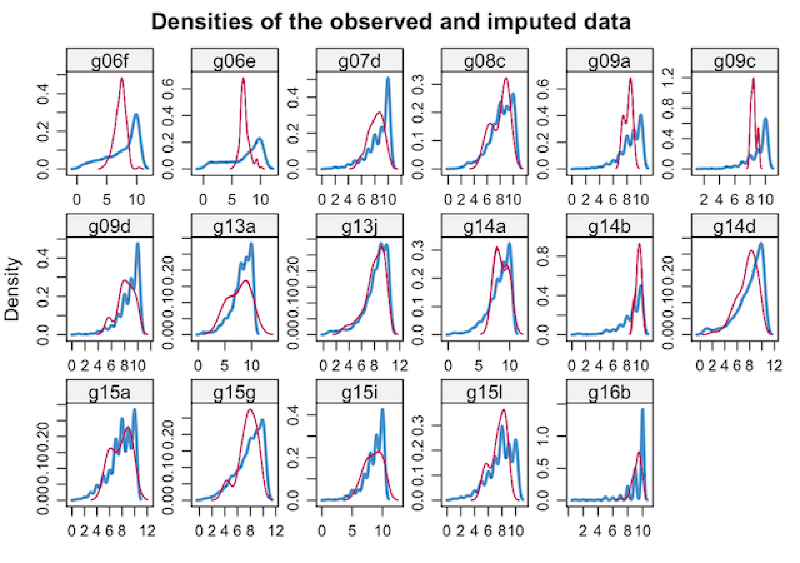
The convention is to plot observed data in blue and the imputed data in red. The figure indicates that the imputed and the observed values fall in the same range. Under MAR, which is our case,they can be different, both in location and spread, but their multivariate distribution is assumed to be identical, and this is quite not the case:
densityplot(rest.imp, main = "Densities of the observed and imputed data")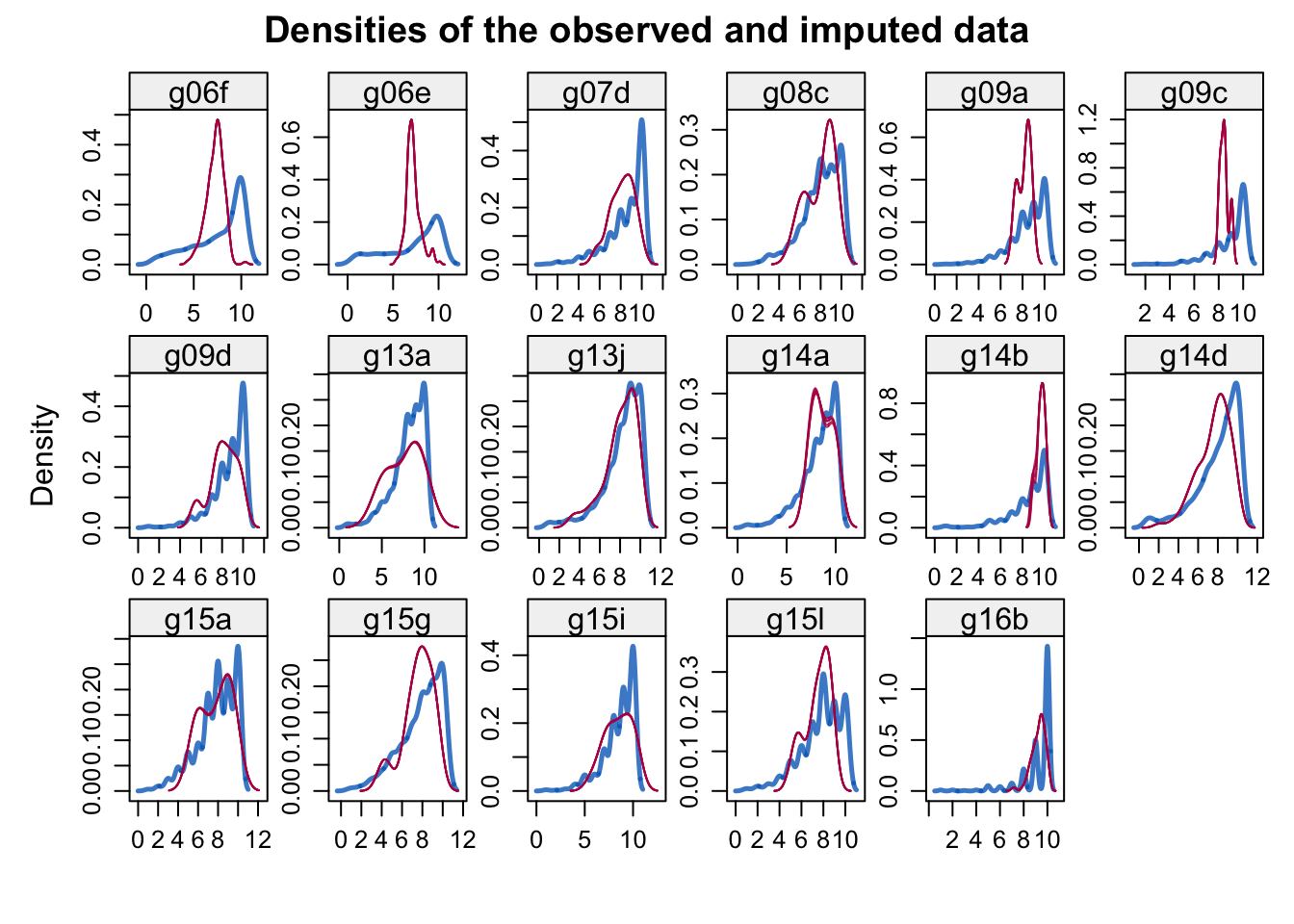
I therefore wanted to investigate more the nature of our missing values, so I’ve decided to create other two imputated datasets using two other different methods, the mean substitution and the predective mean method.
The former consists of replacing any missing value with the mean of that variable for all other cases, which has the benefit of not changing the sample mean for that variable. However, mean imputation attenuates any correlations involving the variables that are imputed, thus it gets problematic in multivariate analysis
The latter aims to reduce the bias introduced in a dataset through imputation, by drawing real values sampled from the data.This is achieved by building a small subset of observations where the outcome variable matches the outcome of the observations with missing values.
By plotting the densities of the observed and imputed data for all the three cases, we see that the PMM is the one that best follow the shape of the observed data.
rest.imp2 <- mice(restaurant, method = "pmm", m = 5, seed = 654)
rest.imp3 <- mice(restaurant, method = "mean", m = 1, seed = 654)library(metaplot)
library(lattice)
norm.imput <- densityplot(rest.imp, ~g06f + g06e + g07d,
main = "Regression Imputation")
pmm.imput <- densityplot(rest.imp2, ~g06f + g06e + g07d,
main = "Predictive Mean Imputation")
mean.imput <- densityplot(rest.imp3, ~g06f + g06e + g07d, main =
"Mean Imputation")
#print the plots
multiplot(norm.imput, mean.imput, pmm.imput, nrow = 3 )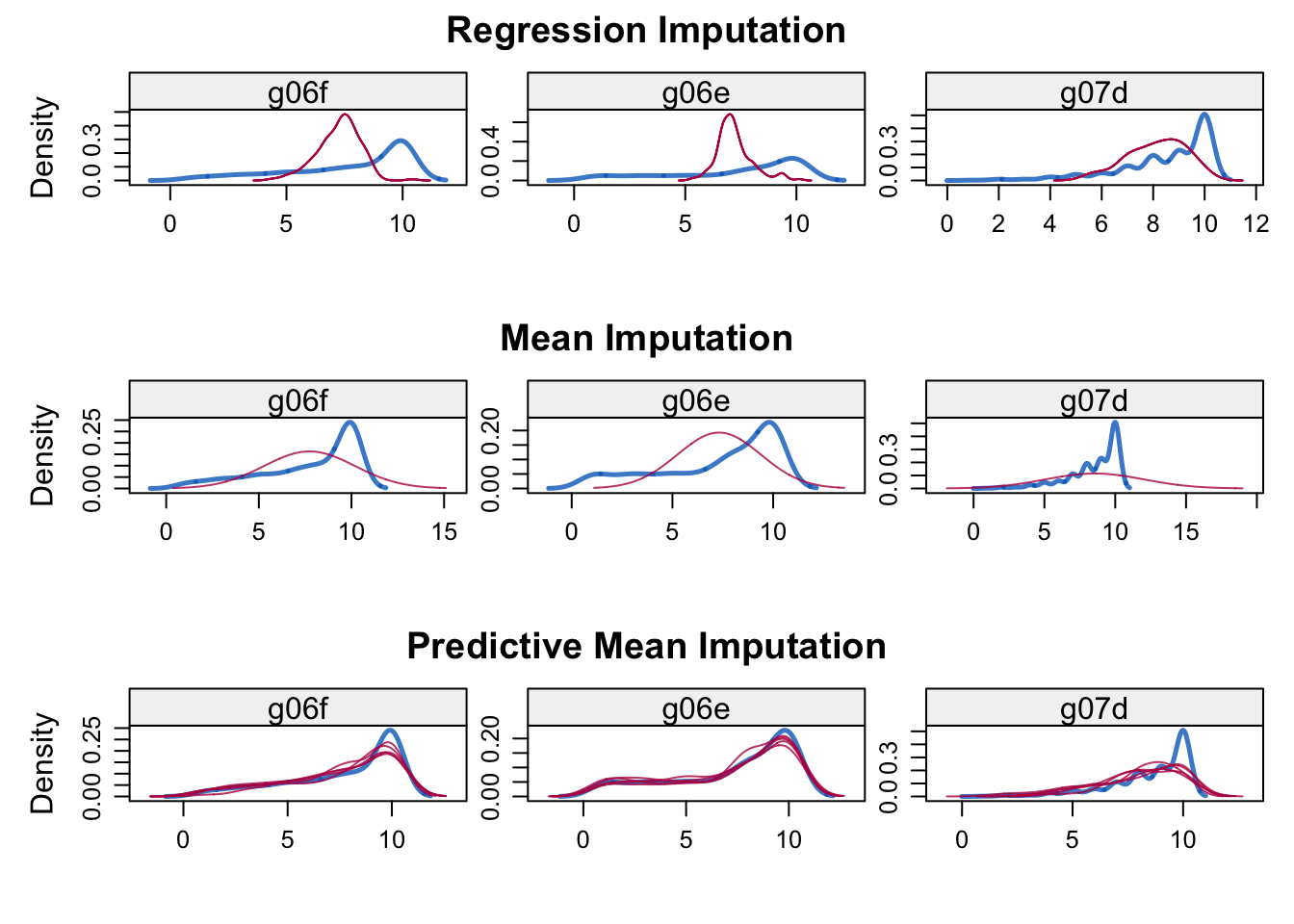
Statistical Analysis
Fitting the Model
Next step consists of fitting the multiple linear regression model over the best imputed dataset, which is the one imputed by PMM.
rest.impfit <- with(rest.imp2, lm(g27a ~
g06f+g06e+g07d+g08c+g09a+g09c+g09d+
g13a+g13j+g14a+g14b+g14d+g15a+g15g+
g15i+g15l+g16b))
#regression model fitted to the first imputed data set (over m=5)
summary(rest.impfit$analyses[[1]])##
## Call:
## lm(formula = g27a ~ g06f + g06e + g07d + g08c + g09a + g09c +
## g09d + g13a + g13j + g14a + g14b + g14d + g15a + g15g + g15i +
## g15l + g16b)
##
## Residuals:
## Min 1Q Median 3Q Max
## -6.1819 -0.4942 0.1310 0.5479 3.0860
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.064186 0.253076 0.254 0.79984
## g06f -0.005775 0.011335 -0.509 0.61054
## g06e -0.008057 0.009645 -0.835 0.40368
## g07d 0.098379 0.021138 4.654 3.68e-06 ***
## g08c 0.034701 0.020982 1.654 0.09847 .
## g09a 0.148122 0.030877 4.797 1.85e-06 ***
## g09c 0.014736 0.025137 0.586 0.55787
## g09d 0.083034 0.030945 2.683 0.00741 **
## g13a 0.200077 0.028223 7.089 2.53e-12 ***
## g13j 0.048094 0.019215 2.503 0.01247 *
## g14a -0.075115 0.027914 -2.691 0.00724 **
## g14b 0.140943 0.028843 4.887 1.19e-06 ***
## g14d 0.087489 0.021389 4.090 4.65e-05 ***
## g15a 0.132695 0.022021 6.026 2.35e-09 ***
## g15g 0.058411 0.018581 3.144 0.00172 **
## g15i -0.009585 0.029052 -0.330 0.74153
## g15l 0.021256 0.019101 1.113 0.26604
## g16b -0.012585 0.023506 -0.535 0.59250
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.9015 on 1015 degrees of freedom
## Multiple R-squared: 0.7027, Adjusted R-squared: 0.6977
## F-statistic: 141.1 on 17 and 1015 DF, p-value: < 2.2e-16restaurantpool <- pool(rest.impfit)
summary(restaurantpool)## term estimate std.error statistic df p.value
## 1 (Intercept) 0.093311999 0.25593471 0.3645930 867.97438 7.155041e-01
## 2 g06f -0.004130195 0.01217619 -0.3392027 202.92081 7.348078e-01
## 3 g06e -0.008842911 0.01178729 -0.7502073 42.02305 4.573099e-01
## 4 g07d 0.092400750 0.02222263 4.1579575 411.80609 3.909001e-05
## 5 g08c 0.028431068 0.02141505 1.3276206 737.13483 1.847145e-01
## 6 g09a 0.152751259 0.03121551 4.8934411 970.30517 1.159728e-06
## 7 g09c 0.016740601 0.02526794 0.6625233 992.74769 5.077897e-01
## 8 g09d 0.079750269 0.03166617 2.5184688 738.84782 1.199677e-02
## 9 g13a 0.207045126 0.02947312 7.0248809 361.35165 1.070832e-11
## 10 g13j 0.039411470 0.02005144 1.9655184 333.65458 5.018336e-02
## 11 g14a -0.068666337 0.02870816 -2.3918754 559.99955 1.709138e-02
## 12 g14b 0.144759002 0.02960123 4.8903037 704.96456 1.248006e-06
## 13 g14d 0.079839750 0.02376921 3.3589563 85.13462 1.172183e-03
## 14 g15a 0.132617943 0.02258510 5.8719223 813.54221 6.272860e-09
## 15 g15g 0.059672214 0.01898461 3.1431883 792.57343 1.733413e-03
## 16 g15i -0.006654477 0.02907106 -0.2289038 926.33462 8.189942e-01
## 17 g15l 0.027437413 0.01988795 1.3796000 434.60711 1.684192e-01
## 18 g16b -0.018946953 0.02393784 -0.7915065 506.07374 4.290193e-01#The pooled fit object is of class "mipo" (multiply imputed pooled object).After fitting the model, it was possible to discover which variables are statistically significant (p-value < 0.01) in assessing the overall quality of a restaurant :
- g07d: Kindly placed at good table
- g09a: Taste of food
- g09d: Quality of ingredients
- g13a: Quality of general service
- g14a: Neat appearance of waiters
- g14b: Friendliness
- g14d: Competent information about food and drinks
- g15a: Atmosphere in the restaurant
- g15g: Air quality/freshness
Diagnostic for goodness of the model
#Model Diagnostic Plot
par(mfrow=c(2,2))
plot(rest.impfit$analyses[[1]], col = "steelblue")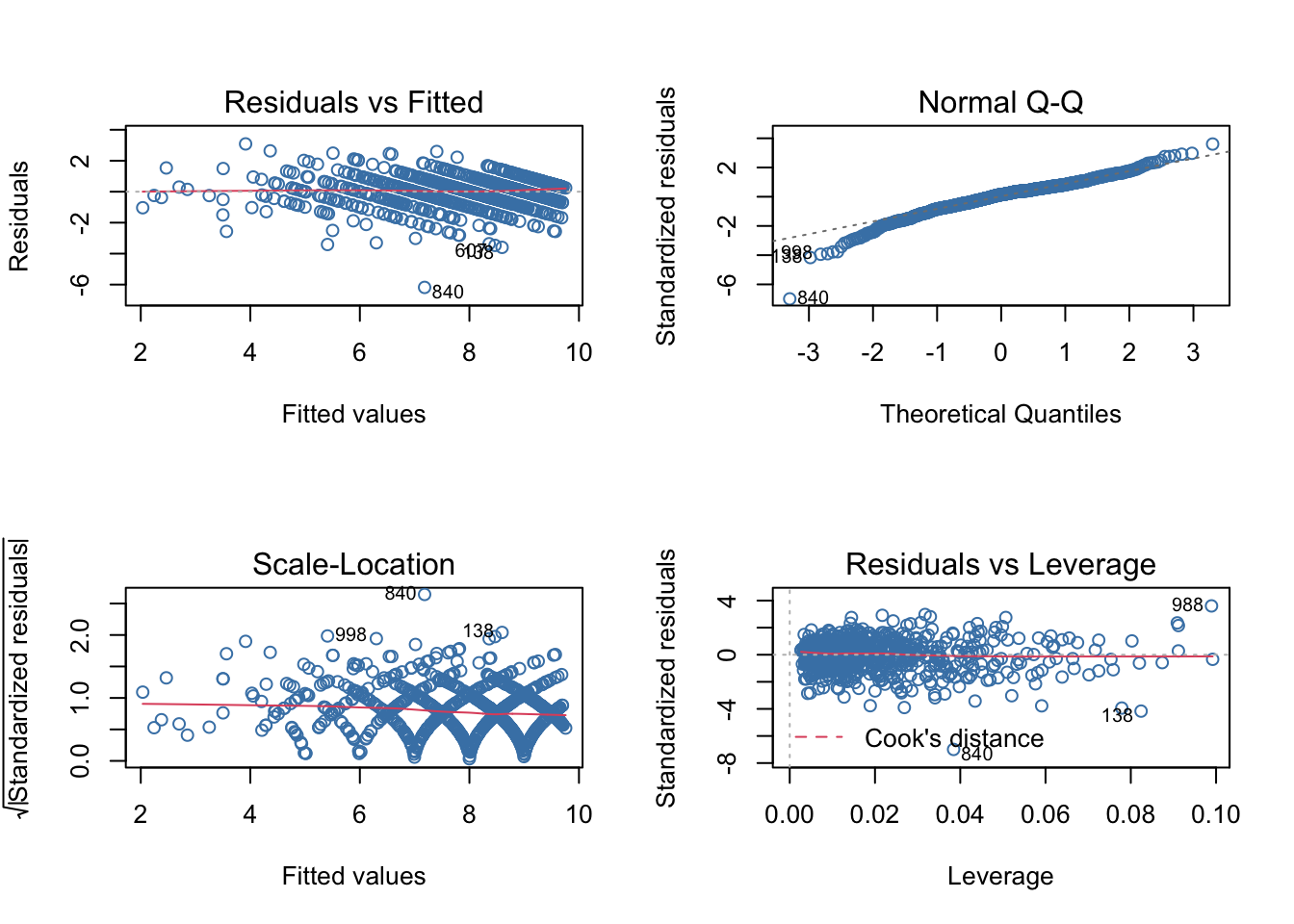
Regression diagnostic: - The first plot is the “Residual vs Fitted”, in which we can observe that the points are almost equally spread along the horizontal line, and so thus suggesting a linear relationship between predictors and outcome variable.
Then we have the “Normal Q-Q” plot, which claim that normality assumption about the residuals is not violated, since they do not deviate much from the straight line, except for just a few outliers, particularly #840.
Following the diagnostic I’ve implemented a “Scale-Location” plot, in which we can see that residuals are spread equally along the rangers of predictors, proof that the homoskedasticity assumption holds.
Finally we have “Residuals vs Leverage” plot, which shows that the value further from the Cook’s distance (so with a high value for Cook’s distance scores) is #840, suggesting that it is influential to regression and that results will be altered if we include it.
## sqloss_ri l1loss_ri
## [1,] 0.9184487 0.6856649## sqloss_imp l1loss_imp
## [1,] 0.9185395 0.6887167Data Visualization
corr <- cor(complete(rest.imp2, 1)[, 2:18])
library(gplots)
rowclust <- hclust(dist(scale(complete(rest.imp2, 1)[, 2:18])),
method = "average")
unicor <- cor(complete(rest.imp2, 1)[, 2:18])
cordist <- 0.5 - unicor / 2
colclust <- hclust(as.dist(cordist), method = "average")
heatmap.2(
corr,
Rowv = as.dendrogram(colclust),
Colv = as.dendrogram(colclust),
scale = "none",
trace = "none",
col = heat.colors,
breaks = 8,
cexCol = 0.6,
cexRow = 0.5,
cellnote = round(unicor, digits = 2),
notecol = "black",
notecex = 1.0)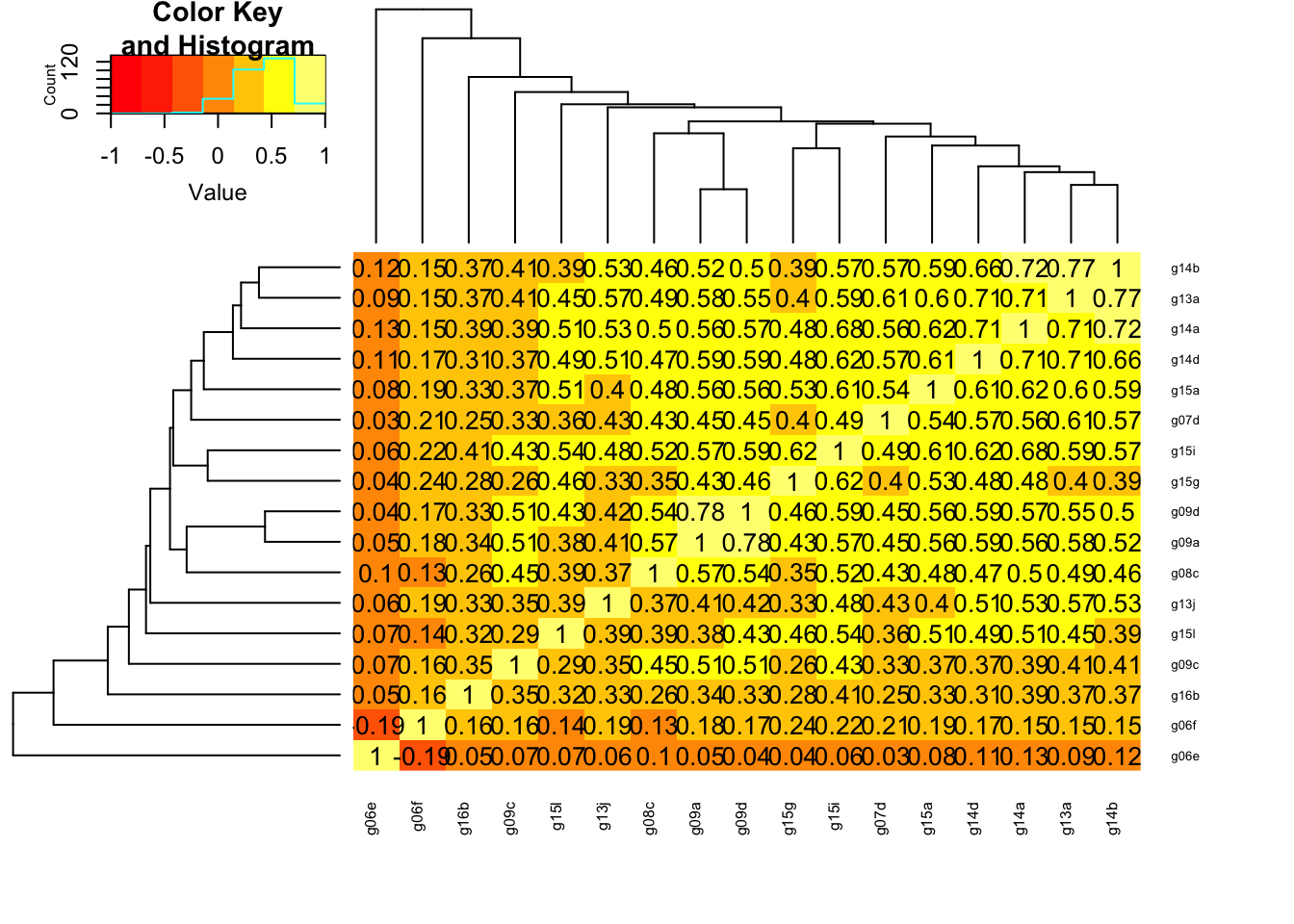
In this plot it can be seen that g06e and g06f are negatively correlated, this can be explained by the fact that variable g06f measure parking situation and instead g06e measures the access to the restaurant with public transport, and so a restaurant with a good parking may be far from city centre and so not well connected by public transport.
The highest correlation is present between g09a and g09d (0.78), taste of food and quality of ingredients, which makes sense.
Then the variable from group of question g14 and g13 and slightly less g15 are highly correlated, which again it makes sense that they are correlated as they refer to common characteristics.
Factor Analysis
Then I decided to carry on a Exploratory Factor Analysis, rather than PCA, as the heatmap suggested an underlying causal structure, to understand whether some of the explanatory variables measure the same thing or are related to the same factor. For the same reason I’ve implemented the oblique factor matrix rotation (rotation = "promax") excluding the variable “g27a” since the focus is exactly to explain “g27a”).
restFA <- complete(rest.imp2,1)[,-1] #excluding 1st col
fit <- factanal(restFA, factors = 9, rotation = "promax") Interpretation
Factors Selection Criteria
test <- data.frame(fit$STATISTIC, fit$PVAL )
colnames(test) <- c("Chi-Squared Goodness-of-fit Statistic", "p-value" )
rownames(test) <- ""
test## Chi-Squared Goodness-of-fit Statistic p-value
## 18.4486 0.4926839To decide how many factors are sufficient to account for the correlations among the original variables we look at the significance level of the \({\chi}^2\) goodness-of-fit statistic that we can find in the output. The null of this test is that 9 factors are sufficient for our model and the p-value proves that there is moderate evidence to not reject \(H0\).
Also from the loadings output I’ve noticed that the SS loading of the 9th factor is low (<< 1), but the cumulative variance explained reach the 60% which I’ve assessed as a good cutoff.
The answer may also be seen graphically by taking a look at the scree-plot of the eigenvalues and counting after how many eigenvalues the line gets flat
barplot(eigen(cor(restFA))$values,
main = "Scree-plot",
xlab = "Eigenvalues",
col ="orange")
lines(x = 1:nrow(as.matrix(eigen(cor(restFA))$values)), eigen(cor(restFA))$values,
type="b", pch=19, col = "black")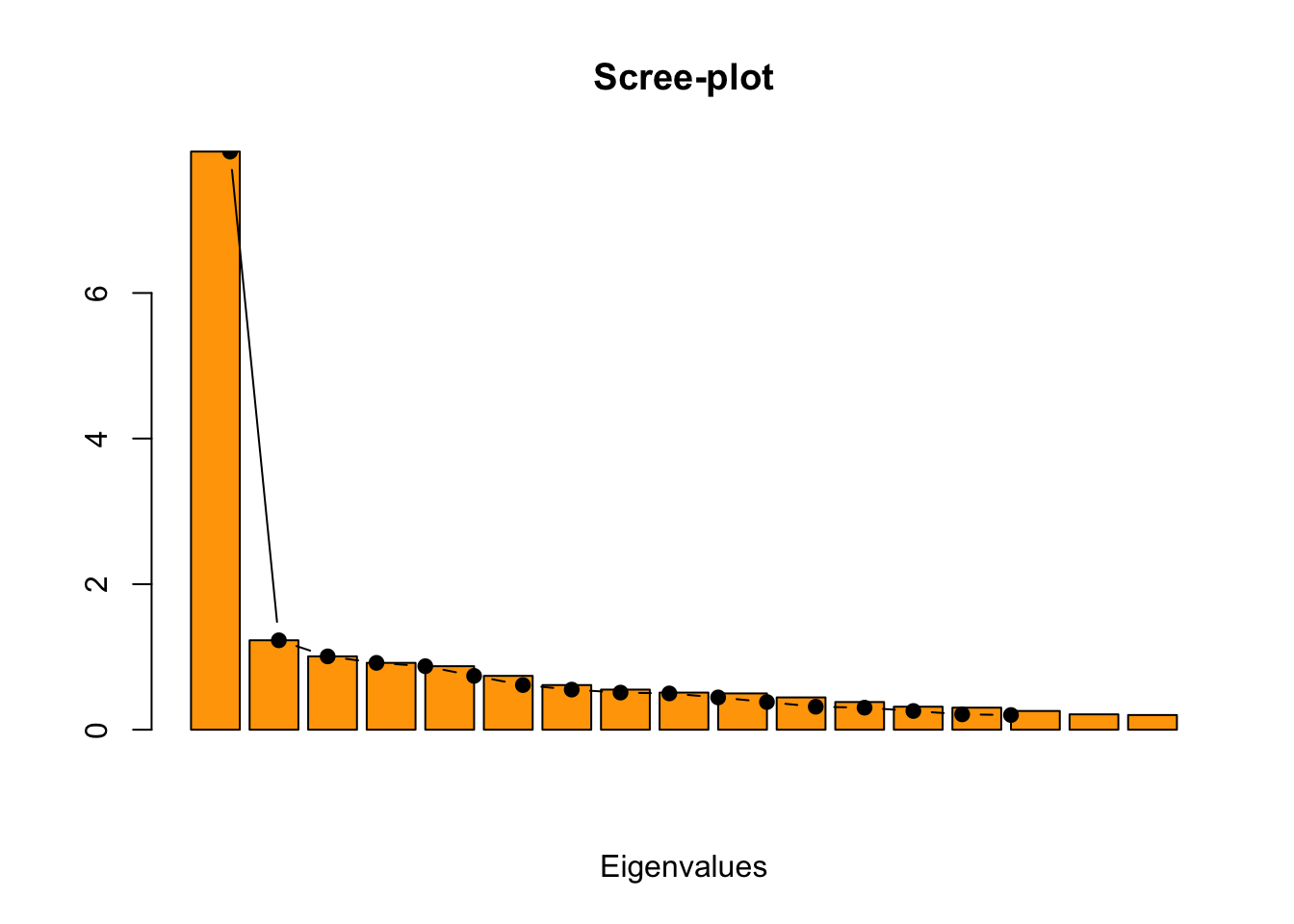
Then, I’ve looked at the uniqueness for selecting the most important variables. A high uniqueness for a variable usually means it doesn’t fit clearly into the factors. If we subtract the uniqueness from 1, we get a quantity called the communality. The communality is the proportion of variance of the \(i-th\) variable contributed by the common factors.
uniq <- round(as.data.frame(cbind(fit$uniquenesses, (1-fit$uniquenesses))), digits = 2)
colnames(uniq) <- c("Uniqueness", "Communalities")
uniq ## Uniqueness Communalities
## g06f 0.56 0.44
## g06e 0.86 0.14
## g07d 0.49 0.51
## g08c 0.00 1.00
## g09a 0.23 0.77
## g09c 0.56 0.44
## g09d 0.18 0.82
## g13a 0.16 0.84
## g13j 0.55 0.45
## g14a 0.16 0.84
## g14b 0.25 0.75
## g14d 0.31 0.69
## g15a 0.00 1.00
## g15g 0.00 1.00
## g15i 0.32 0.68
## g15l 0.38 0.62
## g16b 0.61 0.39As a matter of fact the variables with higher values of uniqueness corresponds to the statistically significant variables in the multiple linear regression model
Factor Loadings
Before interpreting all the loadings, as we’re dealing with 17 variables I’ve set a cutoff for not showing in the output low values and then I’ve selected the variables whose variance is better explained by the extracted factors (communalities > 0.5) described in the previous section
loadings(fit, digits = 2, cutoff = 0.1, sort=TRUE)##
## Loadings:
## Factor1 Factor2 Factor3 Factor4 Factor5 Factor6 Factor7 Factor8 Factor9
## g06f 0.676
## g06e 0.122 -0.372
## g07d 0.622 -0.129 0.126
## g08c 1.020
## g09a 0.109 0.822
## g09c 0.308 0.100 0.429
## g09d 0.920
## g13a 0.976 -0.124
## g13j 0.512 -0.123 0.153 0.182
## g14a 0.543 0.538
## g14b 0.867 -0.196 0.150 0.124
## g14d 0.615 0.205 0.130 -0.153 0.130
## g15a 0.114 0.886
## g15g 1.053
## g15i 0.142 0.188 0.152 0.156 0.200
## g15l 0.817
## g16b 0.617
##
## Factor1 Factor2 Factor3 Factor4 Factor5 Factor6 Factor7 Factor8
## SS loadings 3.093 1.695 1.159 1.077 0.815 0.794 0.707 0.631
## Proportion Var 0.182 0.100 0.068 0.063 0.048 0.047 0.042 0.037
## Cumulative Var 0.182 0.282 0.350 0.413 0.461 0.508 0.549 0.587
## Factor9
## SS loadings 0.393
## Proportion Var 0.023
## Cumulative Var 0.610From the output it appears that the group of variables g13a,g14b,g14a,g14d,g13j shows high correlation with Factor 1 which can be addressed as “Personnel” and it’s also the factor which explain the greatest proportion of variance and with biggest sum of square loadings and so the main important to asses the overall satisfaction with a restaurant
The second factor is highly correlated with the variables g09a,g09c,g09d, which could have been expected as these questions come from the same group, and these could be addressed as Menù, the second most important factor.
The third factor regroup the variables of the group of question g15g, g15i and address the general satisfaction with the Location, of which the main required feature is “Air Quality/Freshness”
Then, I want to move the attention to the 8th factor which refers to Accessibility as the variables that mainly load this factor are g06f,g06e, of which we’ve already checked the negative correlation and for the same reason an increase of “Good Parking Situation” implies a decrease of “Good to Access by Public Transport”
Conclusions
After fitting a multiple linear regression model on the data imputed according the best criteria among regression imputation, mean imputation and predictive mean imputation and after performing an exploratory factor analysis it was possible to have an insight on the main factors when assessing the overall satisfaction with a restaurant: 1. Personnel 2. Menù 3. Location 4. Accessibility
References
[1] Heinzen, E., Sinnwell, J., Atkinson, E., Gunderson, T. and Dougherty, G. (2021). Arsenal: An arsenal of r functions for large-scale statistical summaries.
[2] van Buuren, S. and Groothuis-Oudshoorn, K. (2021). Mice: Multivariate imputation by chained equations.
[3] Tierney, N., Cook, D., McBain, M. and Fay, C. (2021). Naniar: Data structures, summaries, and visualisations for missing data.
[4] Templ, M., Kowarik, A., Alfons, A., de Cillia, G. and Rannetbauer, W. (2021). VIM: Visualization and imputation of missing values.
[5] van Buuren, S. and Groothuis-Oudshoorn, K. (2011). mice: Multivariate imputation by chained equations in r. Journal of Statistical Software 45 1–67.
[6] Kowarik, A. and Templ, M. (2016). Imputation with the R package VIM. Journal of Statistical Software 74 1–16.